今日はとても趣味度が高い、マニアックなお話をしたいと思います。
トロコイド(trochoid)
皆さんも子供の頃遊んだことがあるかもしれません。
または大学受験の数学の問題で触れたことがあるかもしれません。
このトロコイドを、大学数学で学んだ数式処理システム
Mathematicaを用いて、深く見ていきます。
そんな感じの(私にとっては)懐かしいお話です。
Contents
- 1.トロコイド(trochoid)
- 2.トロコイド曲線の方程式の導出
- 3.Mathematicaへの適用
- 4.おまけ
- 5.まとめ
目次
トロコイド(trochoid)
"トロコイド(trochoid)"とは、円をある曲線に沿って滑らないように転がした時、その円の内部又は外部の定点が描く曲線です。
高校の数学の授業でサイクロイド(cycloid)
また応用としてカージオイド(cardioid)などはすべてトロコイドの一種です。
また、子供の頃このような玩具で遊んだことがある人はいませんか?
src="https://dl.dropboxusercontent.com/s/nf2wbxah0qklixl/395-01.jpg">
これはスピログラフと言う、曲線を描く定規です。
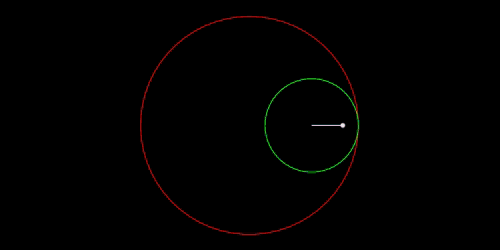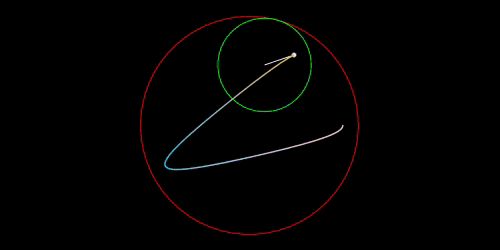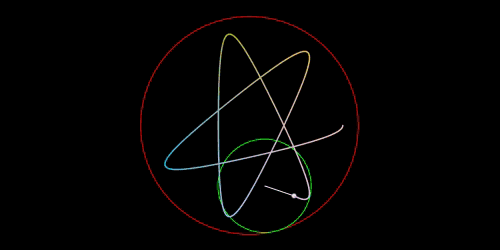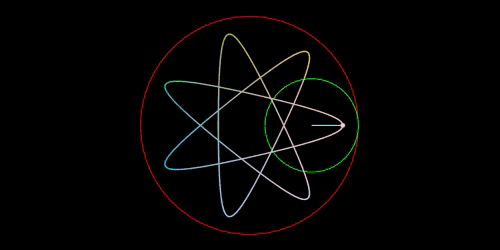
スピログラフで描かれる曲線は万華鏡のような幾何学模様になり、
内トロコイドと言うトロコイドの一種です。
または車好きな方はロータリーエンジン(Rotary Engine)、
バンケルエンジン(Wankel Engine)でも連想できるかもしれません。
この記事ではトロコイドの数式を求め、
実際にMathematicで描いていきたいと思います。
トロコイド曲線の方程式の導出
トロコイド曲線をMathematicaで描くには方程式が必要です。
早速トロコイド曲線の方程式を導き出していきましょう。
(因みに、この章で説明に用いる画像は全てMathematicaで作成しました。)
まず中心:O, 半径=r1 の円C1と,
C1に内接する中心:Q, 半径=r2 の円C2を考えます.
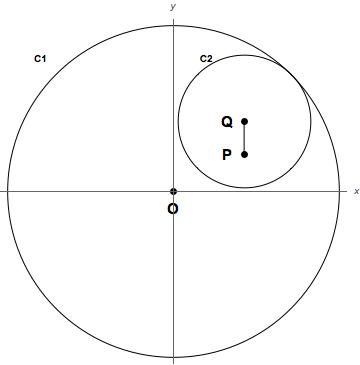
図1
C2の内部に任意の点Pをとり、点Qと点Pとの距離をr3とします.
C2はC1の内部に接しながら滑らず転がります.
このときの点Pの軌跡がスピログラフになります.
第一象限を拡大してみます.
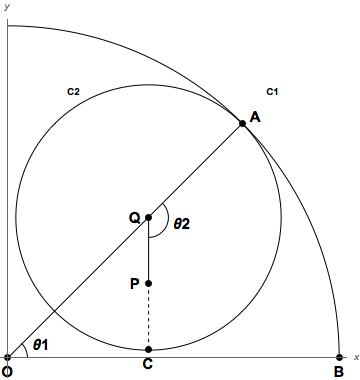
図2
図のように線分OQと円C1との交点をA,
円C1とx軸(x>0)との交点をB,
線分QPと円C2との交点をCとし
角AOBをθ1, 角AQCをθ2とします.
r1, r2, r3, θ1, θ2 を用いると
OP = r1 - r2
であるので円C2の中心Pは
P = ( (r1 - r2)*cosθ1, (r1 - r2)*sinθ1 ) ...(1)
と得られます.
円C2は円C1の内部を滑らず転がるという仮定より,
弧長AB = 弧長CB
が成り立つことから
AB = r1*θ1
CB = r2*θ2
つまり
θ2 = ( r1*θ1 ) /r2 ...(2)
となる.
従って点Qの座標は
Q=( P + r3*cos(θ1 - θ2), P + r3*sin(θ1 - θ2) ) ...(3)
である.
(1),(2)を(3)に代入すると,
Q = { (r1 - r2)*cosθ1 + r3*cos(θ1 - (r1*θ1)/r2), (r1 - r2)*sinθ1 + r3*sin(θ1 - (r1*θ1)/r2) }
が得られます。
これでやっと点Qの軌跡が描けるようになりました。
Mathematicaへの適用
上で求めた方程式を、Mathematicaへ適用させていきます。
まずは点Qの定義です。
[mm]
q[r1_,r2_,r3_,th1_]:={(r1-r2)Cos[th1]+r3*Cos[(1-r1/r2)th1],
(r1-r2)Sin[th1]+r3*Sin[(1-r1/r2)th1]}
[/mm]
上と全く同じ変数を用いています。
図2を思い出してください。
r1 := C1の半径
r2 := C2の半径
r3 := |QP|
th1 := 角AOB
これで4変数に依存する動点Qの座標が求まります。
一見すると変数は4つありますが、その内3つ(r1,r2,r3)は後にユーザーによって任意に固定されます。
なので実際の変数はth1のみです。
次にTable関数を用いて点群をリスト化します。
前にも述べた通り、このプログラムを動かす際に任意にr1,r2,r3を固定する必要があります。
ここでは例として
r1 = 10
r2 = 7
r3 = 5
としました。
またth1を動かしていくのですが、th1を動かすための3つの条件(初期値、終了値、刻み幅)を指定しなければなりません。
ここでは例として
初期値 = 0
終了値 = 20π
刻み幅 = 0.1
としました。
以上をMathematicaで記述すると下記のようになります。
[mm]
Table[q[10,7,5,th1],{th1,0,20Pi,0.1}]
[/mm]
これを実行すると指定した条件でth1を動かした時の点Qの座標がリスト化されます。
最後に上で求めた座標を繋ぎ合わせます。
[mm]
Show[Graphics[Line[Table[q[10,7,5,th1],{th1,0,20Pi,0.1}]]]]
[/mm]
Line関数で点と点を繋ぎ、
Graphics関数で2Dグラフィックスを作成、
Show関数で表示させる
という流れになっています。
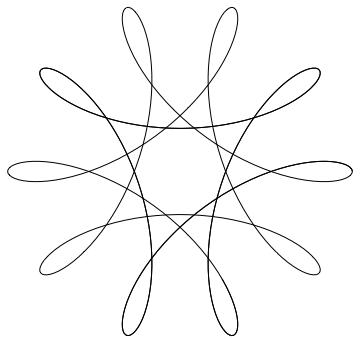
r1=10, r2=7, r3=5
これがr1=10,r2=7,r3=5と固定し、θ1を0から20πまで動かした時のスピログラフです。
とても美しい幾何学模様ですね。
おまけ
最後にスピログラフを簡単に書くためにMathematicaで独自関数を定義しちゃいましょう。
"spiro[ ]" という関数名にします。
(th1の条件は上と全く一緒です。もちろん変更も可能)
[mm]
spiro[r1_,r2_,r3_]:=Show[Graphics[Line[
Table[{(r1-r2)Cos[th1]+r3*Cos[(1-r1/r2)th1],
(r1-r2)Sin[th1]+r3*Sin[(1-r1/r2)th1]},
{th1,0,20Pi,0.1}]]]]
[/mm]
これを一度実行するだけでこれ以降は "sprio[1,2,3]" と打つだけでr1=1,r2=2,r3=3のスピログラフが描けちゃいます。

r1=8, r2=3, r3=2
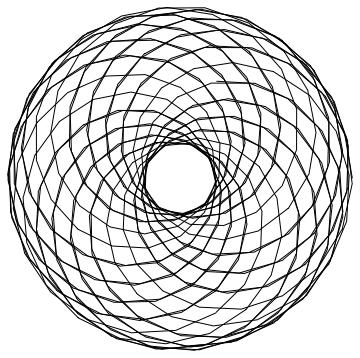
r1=60, r2=1, r3=90
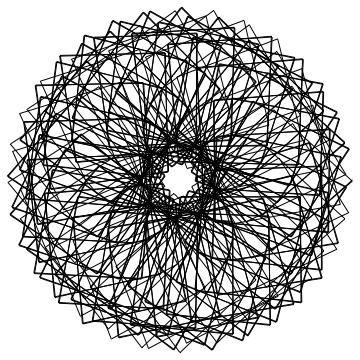
r1=100, r2=6, r3=80
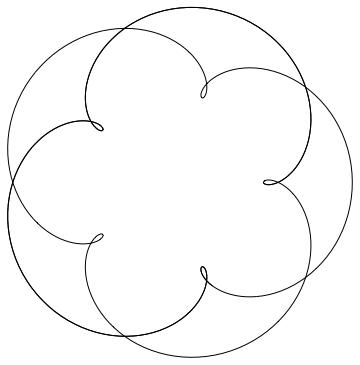
r1=5, r2=7, r3=6
まとめ
幾何学模様は不思議だらけですよね。
同じ数式から刺々しいモノが出たり、丸っこいモノが出たりします。
3変数r1,r2,r3の組み合わせは無限通り、スピログラフの形も無限通り。
と思って3変数をなんども変えて実行してたのですが、
3つの数値を思いっきり変えたとしても似た図形が生成されることがありました。
様々な図形を表示させたい場合は
(すごく当たり前ですけど)3つの数値、というよりは3つの数値の比が大事でした。
少しでも興味を持っていただけたら幸いです。

